使用正则表达式判断二进制数字是否能被3整除
1.摘要
前几天在面试时被问到一个问题:如何用正则表达式判断一个二进制数是否能被3整除。面试时被这个题目问的有些不知所措,回家后想了半天才明白,这实际是一个有关状态机的题目。
2. 问题
写一个正则表达式,匹配所有能被3整除的二进制数。比如:
11 √
110 √
1001 √
1011 ×
3. 整除与余数
判断一个数能否被另一个数整除,可以转化为判断一个数被另一个数除后的余数是否为0。假设被判断的数为N,除数为m,余数为d,那么有:
N=i*m+d
假设有N=abcde=a*x^4+b*x^3+c*x^2+d*x+e,(x为进制)。
同时定义N(0)=0,N(1)=a,N(2)=ab……N(5)=abcde,那么有:
N(0)=0 N(0)%m=0
N(1)=a N(1)%m=a%m
N(2)=a*x+b N(2)%m=(a*x+b)%m
由于取余满足性质:
(1) (a+b)%c = ((a%c)+(b%c))%c;
(2) (a*b)%c = ((a%c)*(b%c))%c;
那么:
N(2)%m=(a*x+b)%m
=((a*x)%m+b%m)%m
=((a%m*x%m)%m+b%m)%m
=((N(1)%m*x%m)%m+b%m)%m
也就是说,判断N是否能被m整除,可以转换为关于N的每一位数字、被除数和进制的递推公式。
4. 余数与状态机
注意到:
1、一个数除以m的余数只有0~m-1这m种可能。
2、一个数的前n位除m的余数可以通过这个数和前n-1位除m的余数求出来。
例如18这个数,写成二进制是10010,要判断它是否能被3整除,那么计算的过程如下:
1 余数为1
10 余数为1*2+0 mod 3=2
100 余数为2*2+0 mod 3=1
1001 余数为1*2+1 mod 3=0
10010 余数为0*2+0=0
可以被整除
这就可以写成是一个关于被除数的每一位数字和被m除后余数之间的状态转换过程,每一个余数是一种状态,而每一位数字是转换的一条边,那么对于除数3来说,余数有0、1、2三种状态,输入有0、1两种。
我们把所有状态都列出来:
| 余数 | 输入 | 结果 |
| 0 | 0 | (0*2+0)%3=0 |
| 0 | 1 | (0*2+1)%3=1 |
| 1 | 0 | (1*2+0)%3=2 |
| 1 | 1 | (1*2+1)%3=0 |
| 2 | 0 | (2*2+0)%3=1 |
| 2 | 1 | (2*2+1)%3=2 |
状态转换图如下:
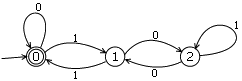
5. 状态机与正则表达式
根据上面的转换图,我们只要把这张转换图所有指向0的边用正则表达式写出来就可以了:
1((10*1)|(01*0))*10*

本作品采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可,转载请注明作者及原网址。
不明觉厉